formula check for curvatures.nb

In the paper there are two ways to calculate K and S
1) using 3x3 solution and Proposition 2.2
2) as eigenvalues of lower 2x2 block of G tensor in Fermi coordinates

In this notebook we show that these two methods coincide.

Define 3x3 solution

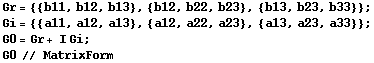
Gr = {{b11, b12, b13}, {b12, b22, b23}, {b13, b23, b33}} ; Gi = {{a11, a12, a13}, {a12, a22, a23}, {a13, a23, a33}} ; G0 = Gr + I Gi ; G0 // MatrixForm

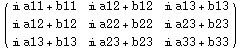
(  a11 + b11  a12 + b12  a13 + b13 ) &# ... + b22  a23 + b23  a13 + b13  a23 + b23  a33 + b33

Define K and S using Proposition 2.2 which gives these
as a function of the 3x3 solution

$(* return adjugate of symmetric matrix *)Adj[mat_] := {{-A23^2 + A22 A33, A13 A23 - A1 ... metric *)Mrand // MatrixForm Norm[Adj[Mrand] - Det[Mrand] Inverse[Mrand]] $

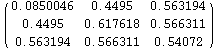
( 0.08500461911758718` 0.44950026359834966` 0.5631943583342383` ) ... 0.5663107173961666` 0.5631943583342383` 0.5663107173961666` 0.5407200124638464`

$p = {1, 0, 0} ; K3[t_] := p . Adj[Greal[t]] . p S3[t_] := -1/2p . (Greal[t] - Tr[Greal[t]] IdentityMatrix[3]) . p$

Define K and S using 2x2 shape operator

$Gsc[t_] := {{G[t][[2]][[2]], G[t][[2]][[3]]},  {G[t][[3]][[2]], G[t][[3]][[3]]}}$

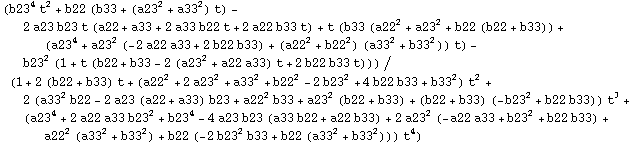
(b23^4 t^2 + b22 (b33 + (a23^2 + a33^2) t) - 2 a23 b23 t (a22 + a33 + 2 a33 b22 t + 2 a22 b33 ... 22 a33 + b23^2 + b22 b33) + a22^2 (a33^2 + b33^2) + b22 (-2 b23^2 b33 + b22 (a33^2 + b33^2))) t^4)

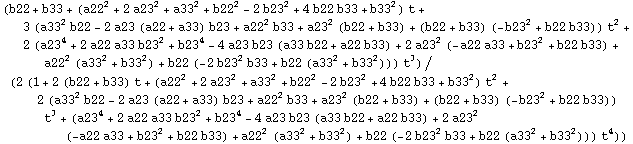
(b22 + b33 + (a22^2 + 2 a23^2 + a33^2 + b22^2 - 2 b23^2 + 4 b22 b33 + b33^2) t + 3 (a33^2 b22 ... 2 a33 + b23^2 + b22 b33) + a22^2 (a33^2 + b33^2) + b22 (-2 b23^2 b33 + b22 (a33^2 + b33^2))) t^4))

Check that different expressions coincide:

Done!

Created by Mathematica (March 10, 2006)